OPERACIONES CON EXPRESIONES ALGEBRAICAS

GRADO: OCTAVO
ÁREA: MATEMATICAS
ASIGNATURA: ALGEBRA
TEMA: UTILIDAD DE LAS OPERACIONES CON EXPRESIONES ALGEBRAICAS
INDICADORES
- Identificar los pasos en las diferentes operaciones de expresiones algebraicas
- Encuentra el área y perímetro de figuras rectangulares utilizando expresiones algebraicas.
- Fórmula explicaciones elementales para socializar sus ideas y comprensión de los diferentes eventos de la realidad.
PALABRAS CLAVES
Matemáticas, algebra, termino, coeficiente, exponente, grado, variable, semejante, polinomio, binomio, monomio, largo, ancho, figura, área, perímetro.
PREGUNTA GENERADORA
¿Cómo identificamos expresiones formales del algebra en el contexto cotidiano?
SITUACION DE APRENDIZAJE
Suma de polinomios algebraico
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
P(x) = 2x3 + 5x − 3 Q(x) = 4x − 3x2 + 2x3
1Ordenamos los polinomios, si no lo están.
Q(x) = 2x3 − 3x2 + 4x
P(x) + Q(x) = (2x3 + 5x − 3) + (2x3 − 3x2 + 4x)
2Agrupamos los monomios del mismo grado.
P(x) + Q(x) = 2x3 + 2x3 − 3 x2 + 5x + 4x − 3
3Sumamos los monomios semejantes.
P(x) + Q(x) = 4x3 − 3x2 + 9x − 3

- También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.
P(x) = 7x4 + 4x2 + 7x + 2 más Q(x) = 6x3 + 8x +3
En el siguiente enlace encuentras la explicación de cada paso para sumar polinomios
http://www.youtube.com/watch?v=oSTi6Mxqj8M
http://www.youtube.com/watch?v=fhMBrzn7VTE&feature=related
Resta de polinomios algebraicos
La resta de polinomios consiste en sumar el opuesto del sustraendo.
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x − 4x − 3
P(x) − Q(x) = 3x2 + x − 3
Observe el desarrollo de los diferentes procesos, asocialos con los recibidos en las diferentes clases.
http://www.youtube.com/watch?v=V3j9rkFYNfY&feature=related
Multiplicación de polinomios
La multiplicación de polinomios es una operación matemática que tiene por objeto obtener un producto a partir de dos expresiones algebraicas denominadas factores.

- Al igual que para la suma en la multiplicación el orden de los factores no altera el producto, denominándose esta característica propiedad conmutativa.

- Los factores de una multiplicación pueden agruparse de cualquier modo demostrando con esto que la multiplicación cumple la ley asociativa.

Leyes de la multiplicación
- Para la multiplicación se hace necesario tener en cuenta la ley de los signos, la cual postula que signos iguales dan un producto positivo y signos diferentes dan un producto negativo.
Detengase y observe con atención el video propuesto
http://www.youtube.com/watch?v=PISqWbVV7P4
http://www.youtube.com/watch?v=ve5gBvV7dIY&feature=related

-
Cuando se multiplican expresiones con la misma denominación es decir la misma letra, el producto se
obtiene dejando la misma letra y sumando sus exponentes.

- El producto de dos términos es el producto de sus coeficientes es decir los números que acompañan a las letras.
Recuerde la observación de los videos es de gran ayuda
http://www.youtube.com/watch?v=TCc-C_Uey2Y&feature=related
http://www.youtube.com/watch?v=SlsUpC9Qm7U&feature=related
HERRAMIENTA DE ANDAMIAJE
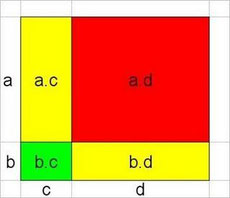


ACTIVIDADES
División de polinomios
Como en el caso de la adición que la resta no se tiene en cuenta por que el signo del monomio determina si
el resultado aumenta o disminuye, en el caso de la multiplicación sucede algo análogo dado que al multiplicar por el inverso se obtiene el mismo resultado que multiplicando.

-
El inverso de un polinomio en este caso es la unidad dividida por el mismo polinomio, el cociente de
esta división se le denomina inverso del polinomio.
Ejemplo:

- En las expresiones algebraicas en las cuales hay fracciones el producto se obtiene multiplicando solamente el numerado por otro factor, si el otro factor también es fraccionario el producto se obtiene multiplicando los numeradores y los denominadores entre si.
Recuerde la observación y elescuchar con atención el video propuesto es aclarar las
dudas presentadas
división de monomios:
http://www.youtube.com/watch?v=U-ErPTjSpmI&feature=related
http://www.youtube.com/watch?v=URfyfKY7mEc&feature=related
división de polinomios
http://www.youtube.com/watch?v=thtodf4hcvE&feature=related
http://www.youtube.com/watch?v=Ml0hrVZNaAw&feature=related
REGLA DE RUFFINNI
II MÉTODO PARA DIVIDIR POLINOMIOS
Paolo Ruffini (1765, 1822) fue un matemático italiano, que establecían un método más breve para hacer la división de polinomios, cuando el divisor es un binomio de la forma x — a.
Regla de Ruffini
Para explicar los pasos a aplicar en la regla de Ruffini vamos a tomar de ejemplo la división:
(x4 − 3x2 + 2 ) : (x − 3)
1. Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.
2. los coeficientes del dividendo en una línea.
3. Abajo a la izquierda colocamos el opuesto del término independendiente del divisor.
4. Trazamos una raya y bajamos el primer coeficiente.
1 0 -3 0 +2
+3
__________________________________
1
5. Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.
1 0 -3 0 +2
+3 3
__________________________________
1 3
6. Sumamos los dos coeficientes.
1 0 -3 0 +2
+3 +3
__________________________________
1 3
7. Repetimos el proceso anterior.
1 0 -3 0 +2
+3 +3 +9
__________________________________
1 3 +6
Volvemos a repetir el proceso.
1 0 -3 0 +2
+3 +3 +9 +18
__________________________________
1 3 +6 +18
Volvemos a repetir.
1 0 -3 0 +2
+3 +3 +9 +18 +54
__________________________________
1 3 +6 +18 +56
8. El último número obtenido, 56 , es el resto.
9.
El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos
obtenido.
x3 + 3 x2 + 6x +18
Teorema del resto
El resto de la división de un polinomio P(x), entre un polinomio de la forma (x − a) es el valor numérico de dicho polinomio para el valor: x = a.
Calcular por el teorema del resto el resto de la división:
P(x) : Q(x)
P(x)= x4 − 3x2 + 2 Q(x) = x − 3
1 0 -3 0 +2
+3 +3 +9 +18 +54
__________________________________
1 3 +6 +18 +56
P(3) = 34 − 3 · 32 + 2 = 81 − 27 + 2 = 56
http://www.youtube.com/watch?v=80MyB6HXAwc&feature=related
DIVISION SINTETICA O METODO DE RUFFINI
ACTIVIDADES
CRITERIOS DE EVALUACION
Se tendrá en cuenta los siguientes criterios:
Puntualidad,
Claridad,
Pertinencia,
Coherencia,
Apropiación de la herramienta, de los conceptos y contenidos en cada actividad.
 JUGANDO CON EL ALGEBRA
JUGANDO CON EL ALGEBRA


